数値演算

数値演算定数

most-positive-fixnum [定数]

#x1fffffff=536,870,911。integerの正の最大値。

most-negative-fixnum [定数]

-#x20000000= -536,870,912。integerの負の最大値

short-float-epsilon [定数]

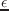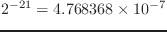IEEEの浮動小数点表現形式であるfloatは、 21ビットの固定小数(うち符号 が1ビット)と7ビットの指数(うち符号が1ビット)で構成されている。 したがって、浮動小数点誤差$\epsilon$は $2^{-21}= 4.768368 \times 10^{-7}$となる。

single-float-epsilon [定数]

short-float-epsilonと同様に 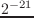$2^{-21}$である。

long-float-epsilon [定数]

Euslispには、doubleもlong floatもないため、 short-float-epsilonと同様に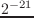$2^{-21}$である。

pi [定数]

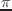$\pi$。 実際には 3.14159203で、 3.14159265ではない。

2pi [定数]

$2\times \pi$。

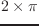pi/2 [定数]

$\pi/2$。

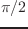-pi [定数]

-3.14159203。

-2pi [定数]

$-2\times \pi$。

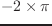-pi/2 [定数]

$-\pi/2$。

比較演算関数

numberp object [関数]

objectがintegerかfloatの時、Tを返す。 その文字が数字で構成されているときも同様である。

integerp object [関数]

objectがintegerの時、Tを返す。 floatはround, truncおよびceiling関数でintegerに変換できる。

floatp object [関数]

object が float の時 T を返す。 integerはfloat関数でfloatに変換できる。

zerop number [関数]

numberがintegerのゼロまたは floatの0.0の時、 Tを返す。

plusp number [関数]

numberが正(ゼロは含まない)のとき、Tを返す。

minusp number [関数]

numberが負のとき、Tを返す。

oddp integer [関数]

integerが奇数のとき、Tを返す。引数はintegerのみ有効。

evenp integer [関数]

integerが偶数のとき、Tを返す。引数はintegerのみ有効。

/= num1 num2 &rest more-numbers [関数]

num1とnum2、more-numbersでどの2つの数値も等しくないとき、Tを返す。それ以外はNILを返す。 num1とnum2、more-numbersを構成する要素はすべて数値であること。

= num1 num2 &rest more-numbers [関数]

num1とnum2、more-numbersがすべて等しいとき、Tを返す。 num1とnum2、more-numbersを構成する要素はすべて数値であること。

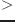$>$ num1 num2 &rest more-numbers [関数]

num1、num2、more-numbersの全要素がこの順に単調減少であるとき、Tを返す。 num1とnum2、more-numbersを構成する要素はすべて数値であること。 誤差を含めた数値比較に対しては、 14章に書かれている関数（eps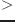$>$）を使用する。

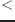$<$ num1 num2 &rest more-numbers [関数]

num1、num2、more-numbersの全要素がこの順に単調増加であるとき、Tを返す。 num1とnum2、more-numbersを構成する要素はすべて数値であること。 誤差を含めた数値比較に対しては、 14章に書かれている関数（eps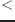$<$）を使用する。

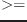$>=$ num1 num2 &rest more-numbers [関数]

num1、num2、more-numbersの全要素がこの順に単調非増加であるとき、Tを返す。 num1とnum2、more-numbersを構成する要素はすべて数値であること。 誤差を含めた数値比較に対しては、 14章に書かれている関数（eps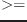$>=$）を使用する。

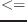$<=$ num1 num2 &rest more-numbers [関数]

num1、num2、more-numbersの全要素がこの順に単調非減少であるとき、Tを返す。 num1とnum2、more-numbersを構成する要素はすべて数値であること。 誤差を含めた数値比較に対しては、 14章に書かれている関数（eps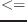$<=$）を使用する。

整数とビット毎の操作関数

以下の関数の引数は、すべてintegerとする。

mod dividend divisor [関数]

dividend を divisorで割った余りを返す。 (mod 6 5)=1, (mod -6 5)=-1, (mod 6 -5)=1, (mod -6 -5)=-1.

1- number [関数]

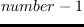$number-1$ を返す。

1+ number [関数]

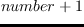$number+1$ を返す。

logand &rest integers [関数]

integersのビット単位ＡＮＤ。

logior &rest integers [関数]

integersのビット単位ＯＲ。

logxor &rest integers [関数]

integersのビット単位ＸＯＲ。

logeqv &rest integers [関数]

logeqvは(lognot (logxor ...))と同等である。

lognand &rest integers [関数]

integersのビット単位ＮＡＮＤ。

lognor &rest integers [関数]

integersのビット単位ＮＯＲ。

lognot integer [関数]

integerのビット反転。

logtest integer1 integer2 [関数]

(logand integer1 integer2)がゼロでないとき T を返す。

logbitp index integer [関数]

integerがNILでなければ、LSBから数えて index番目の ビットが 1 のとき T を返す。

ash integer count [関数]

数値演算左シフト。 もし count が正のとき、integerを左にシフトする。 もし count が負のとき、 integer を $\vert$count$\vert$ ビット右にシフトする。

ldb target position &optional (width 8) [関数]

LoaD Byte. ldb や dpb のByte型は、 EusLispにないため、代りに 2個の integer を使用する。 target のLSBよりposition番目の位置からMSBへ width ビットの 範囲を抜き出す。例えば、 (ldb #x1234 4 4) は 3となる。

dpb value target position &optional (width 8) [関数]

DePosit Byte. targetのLSBよりposition番目の位置へvalueを widthビット置き換える。

一般数値関数

+ &rest numbers [関数]

numbersの和を返す。

- num &rest more-numbers [関数]

もし more-numbers が与えられたとき、numより引く。 そうでないとき、num は符号反転される。

* &rest numbers [関数]

numbersの積を返す。

/ num &rest more-numbers [関数]

num を、more-numbersで割り算する。 num のみ渡された場合、1.0をnumで割り算する。 全ての引数がintegerのとき、integerを返し、 引数に1つでもfloatがあったときは、floatを返す。

abs number [関数]

numberの絶対値を返す。

round number [関数]

numberの小数第1位を四捨五入し integerを返す。 (round 1.5)=2, (round -1.5)=-2.

floor number [関数]

numberの小数を切捨てる。 (floor 1.5)=1, (floor -1.5)=-2.

ceiling number [関数]

numberの小数を切り上げる。 (ceiling 1.5)=2, (ceiling -1.5)=-1.

truncate number [関数]

numberが正のときは切捨て、負のときは切り上げる。 (truncate 1.5)=1, (truncate -1.5)=-1.

float number [関数]

numberをfloatにして返す。

max num &rest more-numbers [関数]

numとmore-numbersの中から、最大値をさがす。

min num &rest more-numbers [関数]

numとmore-numbersの中から、最小値をさがす。

make-random-state &optional (state *random-state*) [関数]

random関数のrandstateのためのrandom-stateオブジェクトを返す。 もし state がrandom-stateのとき、そのオブジェクトのコピーを返す。 stateがTのとき、ランダムに初期化された新たなオブジェクトを返す。 そうでないとき、現在の*random-state*のコピーを返す。

random range &optional (state *random-state*) [関数]

0あるいは0.0 から rangeまでの乱数を返す。 もし range が integerのとき、 integer に変換して返す。 そうでないとき、float を返す。 オプションのstate は、決まった乱数列で表される。 randstateに特別なデータの型はなく、 2つの要素からなる 整数ベクトルで表される。

incf variable &optional (increment 1) [マクロ]

variable は一般の変数である。 variable は、incrementだけ増加され、 variableに戻される。

decf variable &optional (decrement 1) [マクロ]

variable は一般の変数である。 variable は、decrementだけ減少され、 variableに戻される。

reduce func seq [関数]

2変数操作のfunc関数を用いて、seqの中の全ての要素を結合させる。 例えば、(reduce #'expt '(2 3 4)) = (expt (expt 2 3) 4)=4096.

rad2deg radian [関数]

ラジアン値を 度数表現に変換する。 #R は同じものである。 EusLisp の中での角度の表記はラジアンであり、 EusLisp 内の全ての関数が要求する角度引数は、ラジアン表現である。

deg2rad degree [関数]

角度値をラジアン表現に変換する。 また #D でも実行できる。

基本関数

sin theta [関数]

theta はラジアンで表される float 値。 $\sin(theta)$を返す。

cos theta [関数]

theta はラジアンで表される float 値。 $\cos(theta)$を返す。

tan theta [関数]

theta はラジアンで表される float 値。 $\tan(theta)$を返す。

sinh x [関数]

hyperbolic sine、 $\frac{e^{x}-e^{-x}}{2}$で表される。

cosh x [関数]

hyperbolic cosine、 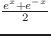$\frac{e^{x}+e^{-x}}{2}$で表される。

tanh x [関数]

hyperbolic tangent、 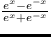$\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$で表される。

asin x [関数]

arc sine.

acos x [関数]

arc cosine.

atan y &optional x [関数]

atan が1つの引数だけのとき、arctangent を計算する。 2つの引数のとき、atan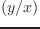$(y/x)$ を計算する。

asinh x [関数]

hyperbolic arc sine.

acosh x [関数]

hyperbolic arc cosine.

atanh x [関数]

hyperbolic arc tangent.

sqrt number [関数]

number の平方根を返す。

log number &optional base [関数]

number の自然対数を返す。 baseが渡された時、baseに対するnumberの対数を返す。

exp x [関数]

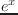$e^{x}$を返す。

expt a x [関数]

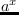$a^{x}$を返す。

拡張された数字

ratio [クラス]

  :super   extended-number 

  :slots 		 (numerator denominator) 

有理数を記述する。

:init num denom [メソッド]

有理数のインスタンスを、分子num分母denomとして初期化する。

complex [クラス]

  :super   extended-number 

  :slots 		 (real imaginary) 

複素数を記述する。

:init re im [メソッド]

複素数のインスタンスを、実部re虚部imとして初期化する。