実数ベクトル(float-vector)

float-vectorは、要素が実数である1次元ベクトルである。 float-vectorは、どんなサイズでも良い。 resultが引き数リストで指定されているとき、 そのresultはfloat-vectorであるべきである。

float-vector &rest numbers [関数]

numbersを要素とするfloat-vectorを新しく作る。 (float-vector 1 2 3)と#F(1 2 3)の違いに注意すること。 前者は、呼ばれたときはいつでもベクトルが生成されるが、 後者は読み込まれたときのみ生成される。

float-vector-p obj [関数]

objがfloat-vectorであるならば、Tを返す。

v+ fltvec1 fltvec2 &optional result [関数]

2つのfloat-vectorを加える。

v- fltvec1 &optional fltvec2 result [関数]

2つのfloat-vectorを差し引く。もし、fltvec2が省略されているならば、 fltvec1の符号が反転される。

v. fltvec1 fltvec2 [関数]

2つのfloat-vectorの内積を計算する。

v* fltvec1 fltvec2 &optional result [関数]

2つのfloat-vectorの外積を計算する。

v.* fltvec1 fltvec2 fltvec3 [関数]

スカラー3重積を計算する。(v.* A B C)=(V. A (V* B C))=(V. (V* A B) C)

v$<$ fltvec1 fltvec2 [関数]

もし、fltvec1の要素がfltvec2の対応する要素よりすべて小さいとき、 Tを返す。

v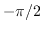$>$ fltvec1 fltvec2 [関数]

もし、fltvec1の要素がfltvec2の対応する要素よりすべて大きいとき、 Tを返す。

vmin &rest fltvec [関数]

fltvecの中のそれぞれの次元における最小値を捜し、 その値でfloat-vectorを新しく作る。vminとvmaxは、 頂点の座標から最小のminimal-boxを見つけるために使用される。

vmax &rest fltvec [関数]

fltvecの中のそれぞれの次元における最大値を捜し、 その値でfloat-vectorを新しく作る。

minimal-box v-list minvec maxvec [err] [関数]

与えられたv-listに対してminimal bounding boxを計算し、 その結果をminvecとmaxvecに蓄積する。 もし、実数errが指定されているならば、minimal boxはその比率によって 成長する。すなわち、もしerrが0.01のとき、minvecのそれぞれの 要素はminvecとmaxvecとの距離の1%減少する。 そして、maxvecのそれぞれの要素は1%増加する。 minimal-boxは、minvecとmaxvecとの距離を返す。

scale number fltvec &optional result [関数]

fltvecのすべての要素をスカラーnumber倍する。

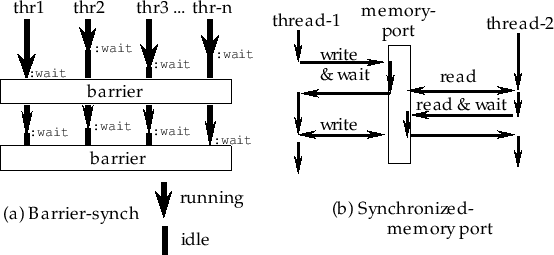
norm fltvec [関数]

fltvecのノルムを求める。 $\Vert fltvec\Vert$

norm2 fltvec [関数]

fltvecのノルムの２乗を求める。 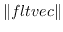$\Vert fltvec\Vert^2$=(v. fltvec fltvec)

normalize-vector fltvec &optional result [関数]

fltvecのノルムが1.0となるように正規化する。

distance fltvec1 fltvec2 [関数]

2つのfloat-vectorの距離を返す。 $\vert fltvec-fltvec2\vert$

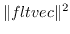
distance2 fltvec1 fltvec2 [関数]

2つのfloat-vectorの距離の2乗を返す。 $\vert fltvec-fltvec2\vert^2$

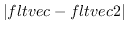
homo2normal homovec &optional normalvec [関数]

同次ベクトルhomovecを正規表現に変換する。

homogenize normalvec &optional homovec [関数]

正規ベクトルnormalvecを同次表現に変換する。

midpoint p p1 p2 &optional result [関数]

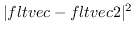pは実数で、p1,p2は同次元のfloat-vectorである。 p1$-$p2を$p:(1-p)$の比率で等分した点 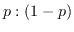$(1-p)\cdot p1 + p\cdot p2$ を返す。

rotate-vector fltvec theta axis &optional result [関数]

2次元あるいは3次元のfltvecをaxis回りにthetaラジアン 回転する。 axisは、:x, :y, :z, 0, 1, 2, または NILの内の一つである。 axisがNILのとき、fltvecは2次元として扱われる。 3次元空間の任意の軸の回りにベクトルを回転するためには、 rotation-matrixで回転行列を作り、そのベクトルにかければよい。