行列と変換

行列は、要素がすべて実数の2次元の配列である。 ほとんどの関数において行列はどんなサイズでもよいが、 v*, v.*, euler-angle, rpy-angle関数では3次元の行列のみ 扱うことができる。 transform, m*とtransposeは、行列を正方行列に限定せず、 一般のn*m行列に対して処理を行う。

resultパラメータを受けた関数は、計算結果をそこに置く。 そのため、ヒープは使用しない。 すべての行列関数は、正規座標系における変換を考慮しており、 同次座標系は考慮していない。

rpy-angle関数は、回転行列をワールド座標系におけるz,y,x軸回りの 3つの回転角に分解する。 euler-angle関数はrpy-angleと同様に分解するが、 回転軸がローカル座標系のz,y,z軸となっている。 角度が反対方向にも得られるため、これらの関数は2つの解を返す。

; Mat is a 3X3 rotation matrix.
(setq rots (rpy-angle mat))
(setq r (unit-matrix 3))
(rotate-matrix r (car rots) :x t r)
(rotate-matrix r (cadr rots) :y t r)
(rotate-matrix r (caddr rots) :z t r)
;--> resulted r is equivalent to mat

3次元空間の位置と方向の組みを保つために、節に記載されている coordinatesとcascaded-coordsクラスを使用すること。

matrix &rest elements [関数]

elementsから行列を新しく作る。 Row x Col = (elementsの数) x (最初のelementの長さ) elementsは、どの型の列((list 1 2 3)や(vector 1 2 3)や (float-vector 1 2 3))でもよい。 それぞれの列は行列の行ベクトルとしてならべられる。

make-matrix rowsize columnsize &optional init [関数]

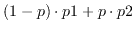$rowsize \times columnsize$の大きさの行列を作る。

matrixp obj [関数]

もし、objが行列のとき、すなわち、objが2次元の配列で その要素が実数であるとき、Tを返す。

matrix-row mat row-index [関数]

行列matからrow-indexで示される行ベクトルを抽出する。 matrix-rowは、setfを使用することにより 行列の特定の行にベクトルを設定することにも使用される。

matrix-column mat column-index [関数]

行列matからcoloumn-indexで示される列ベクトルを抽出する。 matrix-columnは、setfを使用することにより 行列の特定の列にベクトルを設定することにも使用される。

m* matrix1 matrix2 &optional result [関数]

matrix1とmatrix2の積を返す。

transpose matrix &optional result [関数]

matrixの転置行列を返す。すなわち、matrixの列と行を入れ替える。

unit-matrix dim [関数]

dim 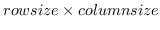$\times$ dimの単位行列を作る。

replace-matrix dest src [関数]

行列destのすべての要素を同一な行列srcで置き換える。

scale-matrix scalar mat [関数]

matのすべての要素にscalerを掛ける。

copy-matrix matrix [関数]

matrixのコピーを作る。

transform matrix fltvector &optional result [関数]

行列matrixをベクトルfltvectorの左から掛ける。

transform fltvector matrix &optional result [関数]

行列matrixをベクトルfltvectorの右から掛ける。

rotate-matrix matrix theta axis &optional world-p result [関数]

rotate-matrixで行列matrixを回転させるとき、 回転軸（:x, :y, :zまたは0,1,2）はワールド座標系あるいは ローカル座標系のどちらかを与えられる。 もし、world-pにNILが指定されているとき、 ローカル座標系の軸に沿った回転を意味し、回転行列を左から掛ける。 もし、world-pがnon-NILのとき、 ワールド座標系に対する回転行列を作り、回転行列を右から掛ける。 もし、axisにNILが与えられたとき、行列matrixは2次元と仮定され、 world-pの如何にかかわらず2次元空間の回転が与えられる。

rotation-matrix theta axis &optional result [関数]

axis軸回りの2次元あるいは3次元の回転行列を作る。 軸は:x,:y,:z,0,1,2,3次元ベクトルあるいはNILのどれかである。 2次元回転行列を作るとき、axisはNILでなければならない。

rotation-angle rotation-matrix [関数]

rotation-matrixから等価な回転軸と角度を抽出し、 実数とfloat-vectorのリストを返す。 rotation-matrixが単位行列のとき、NILが返される。 また、回転角が小さいとき、結果がエラーとなる。 rotation-matrixが2次元のとき、1つの角度値が返される。

rpy-matrix ang-z ang-y ang-x [関数]

ロール、ピッチ、ヨー角で定義される回転行列を作る。 最初に、単位行列をx軸回りにang-xラジアン回転させる。 次に、y軸回りにang-yラジアン、最後にｚ軸回りにang-z ラジアン回転させる。 すべての回転軸はワールド座標系で与えられる。

rpy-angle matrix [関数]

matrixの2組のロール、ピッチ、ヨー角を抽出する。

Euler-matrix ang-z ang-y ang2-z [関数]

3つのオイラー角で定義される回転行列を作る。 最初に単位行列をz軸回りにang-z回転させ、次にy軸回りにang-y 回転させ、最後にz軸回りにang2-z回転させる。 すべての回転軸はローカル座標系で与えられる。

Euler-angle matrix [関数]

matrixから2組のオイラー角を抽出する。