vplus vector-list [関数]
-
-
vector-listのすべての要素の合計を実数ベクトルとして
新しく作り、返す。
v+との違いは、vplusが2つ以上の引数について合計を計算し、
結果のベクトルが指定できない点である。
vector-mean vector-list [関数]
-
-
vector-listの平均ベクトルを返す。
triangle a b c &optional (normal #f(0 0 1)) [関数]
-
-
a, b, cは、2次元または3次元の実数ベクトルである。
normalは、a,b,cが置かれる平面の正規ベクトルである。
triangleはa,b,cで形作られる三角形の領域の2倍の大きさを返す。
normalと同じ方向から見たときにa,b,cが時計方向に回転する
ならば、triangleは正である。
言い換えると、もしtriangleが正ならば、
cはa-bの線分の左手側に位置し、
bはa-cの右手側に位置している。
triangle-normal a b c [関数]
-
-
a b cで定義される三角形に対して垂直方向の正規ベクトルを見つける。
vector-angle v1 v2 &optional (normal (v* v1 v2)) [関数]
-
-
2つのベクトルの角度を計算する。
これは次の式であらわされるatan(normal
 (v1
(v1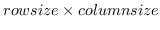 v2), v1
v2), v1 v2)。
v1,v2とnormalは正規ベクトルでなければならない。
normalが与えられないとき、v1,v2の共通垂線の正規ベクトルが
使用される。この場合、結果は0から
v2)。
v1,v2とnormalは正規ベクトルでなければならない。
normalが与えられないとき、v1,v2の共通垂線の正規ベクトルが
使用される。この場合、結果は0から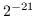 までの範囲の正の角度になる。
符号付きの角度を得るためには、normalを指定しなければならない。
までの範囲の正の角度になる。
符号付きの角度を得るためには、normalを指定しなければならない。
face-normal-vector vertices [関数]
-
-
同じ平面の上にあるベクトルのリストから面の正規化ベクトルを計算する。
farthest p points [関数]
-
-
3次元ベクトルのリストpointsの中からpより最も遠い点を捜す。
farthest-pair points [関数]
-
-
3次元ベクトルのリストpointsからもっとも遠い点の組を
捜す。
maxindex 3D-floatvec [関数]
-
-
3D-floatvecの3つの要素の中で絶対値が最大の要素の位置を捜す。
random-vector &optional (range 1.0) [関数]
-
-
3次元デカルト空間の中で同次的に分散されるランダムベクトルを発生する。
random-normalized-vector &optional (range 1.0) [関数]
-
-
3次元の正規化ランダムベクトルを返す。
random-vectors count range [関数]
-
-
rangeの大きさのランダムベクトルをcount個つくり、そのリストを返す。
line-intersection p1 p2 p3 p4 [関数]
-
-
p1, p2, p3, p4は、すべて2次元以上の実数ベクトルである。
p1-p2とp3-p4が平面上の2つの線分として定義される。
line-intersectionは、これらの2つの線分の交差する点のパラメータ(線分に置ける
交点の位置の比率)を2要素のリストで返す。3次元で使用するとき、
p1, p2, p3, p4は共通平面内になければならない。
collinear-p p1 p2 p3 &optional tolerance [関数]
-
-
p1, p2, p3は、すべて3次元の実数ベクトルで3つの点を表現している。
collinear-pは、もし
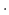 ((p2
((p2 p1)
p1)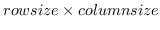 (p3
(p3 p1))
p1))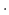 が
*coplanar-threshold*より小さければ、p1-p3の線分の上に
p2を投影したときのパラメータを返す。そうでなければ、NILを返す。
が
*coplanar-threshold*より小さければ、p1-p3の線分の上に
p2を投影したときのパラメータを返す。そうでなければ、NILを返す。
find-coplanar-vertices p1 p2 p3 vlist [関数]
-
-
p1, p2, p3は、3次元の実数ベクトルで、この3つのベクトルから平面を表現している。
find-coplanar-verticesは、その平面内にある点を
vlistの中から捜す。
find-connecting-edge vertex edgelist [関数]
-
-
vertexに接続されたedgelistの中からエッジを捜す。
make-vertex-edge-htab bodfacs [関数]
-
-
bodfacsは、bodyあるいはfaceのリストである。
make-vertex-edge-htabは、bodfacsの中の頂点を抽出し、それに接続されるエッジの検索ができる
ハッシュテーブルを作る。
left-points points p1 p2 normal [関数]
-
-
points, p1, p2は、正規化ベクトルnormalで表現される
平面内にあるものと仮定する。
left-pointsは、p1, p2間の線分の左側に置かれている点を
pointsの中から捜し、集める。
right-points points p1 p2 normal [関数]
-
-
points, p1, p2は、正規化ベクトルnormalで表現される
平面内にあるものと仮定する。
right-pointsは、p1, p2間の線分の右側に置かれている点を
pointsの中から捜し、集める。
left-most-point points p1 p2 normal [関数]
-
-
points, p1, p2は、正規化ベクトルnormalで表現される
平面内にあるものと仮定する。
left-most-pointsは、p1, p2で決定される線分の左側に置かれている点を
pointsの中から捜し、その中でもっとも遠い点を返す。
right-most-point points p1 p2 normal [関数]
-
-
points, p1, p2は、正規化ベクトルnormalで表現される
平面内にあるものと仮定する。
right-most-pointsは、p1, p2で決定される線分の右側に置かれている点を
pointsの中から捜し、その中でもっとも遠い点を返す。
eps= num1 num2 [(tolerance *epsilon*)] [関数]
-
-
2つの実数num1とnum2を比較して、torelanceの誤差範囲内で
等しいかどうかを返す。
eps num1 num2 [(tolerance *epsilon*)] [関数]
num1 num2 [(tolerance *epsilon*)] [関数]
-
-
num1が明らかにnum2よりも小さいときTを返す。すなわち、
num1
 num2-toleranceである。
num2-toleranceである。
eps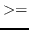 num1 num2 [(tolerance *epsilon*)] [関数]
num1 num2 [(tolerance *epsilon*)] [関数]
-
-
num1が多分num2よりも小さいときあるいは等しいときTを返す。すなわち、
num1
 num2+toleranceである。
num2+toleranceである。
eps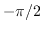 num1 num2 [(tolerance *epsilon*)] [関数]
num1 num2 [(tolerance *epsilon*)] [関数]
-
-
num1が明らかにnum2よりも大きいときTを返す。すなわち、
num1
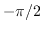 num2+toleranceである。
num2+toleranceである。
eps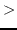 num1 num2 [(tolerance *epsilon*)] [関数]
num1 num2 [(tolerance *epsilon*)] [関数]
-
-
num1が多分num2よりも大きいときあるいは等しいときTを返す。すなわち、
num1
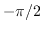 num2-toleranceである。
num2-toleranceである。
bounding-box [クラス]
:super object
:slots (minpoint maxpoint)
-
- xy-,yz-やzx-平面に平行な面を境界とする最小の四角柱を定義する。
bounding-boxは、初期に与えられるベクトルの次元によって、
どんな次元でも使用することができる。
bounding-boxは、surrounding-boxの名前で定義されていた。
:box [メソッド]
-
- このbounding-boxのオブジェクト自身を返す。
:volume [メソッド]
-
- このbounding-boxの体積を返す。
:grow rate [メソッド]
-
-
このbounding-boxのサイズをrate率で増加または減少させる。
rateが0.01のとき、1%拡大される。
:inner point [メソッド]
-
-
pointがこのbounding-box内にあればTを返し、
そうでないときはNILを返す。
:intersection box2 &optional tolerance [メソッド]
-
-
このbounding-boxとbox2との共通bounding-boxを返す。
もし、torelanceが与えられたならば、このboxはその誤差で拡大される。
もし、共通部分がなければ、NILを返す。
:union box2 [メソッド]
-
-
このbounding-boxとbox2を結合したbounding-boxを返す。
:intersectionp box2 [メソッド]
-
-
このbounding-boxとbox2との間に共通領域があればTを返し、
そうでなければNILを返す。
このメソッドは、:intersectionよりも速い。なぜなら、新しい
bounding-boxのインスタンスを作らないためである。
:extreme-point direction [メソッド]
-
-
このbounding-boxの8つの頂点の中で、directionとの内積が最大のものを
返す。
:corners [メソッド]
-
-
このbounding-boxのすべての頂点のリストを返す。
もし、このboxが2次元であれば、4点が返される。
同様に3次元の場合、8点が返される。
:below box2 &optional (direction #(0 0 1) [メソッド]
-
-
このbounding-boxがbox2に対してdirectionの示すベクトル
の下の方向にあればTを返す。
このboundign-boxがdirectionの方向に動かされるとき、
2つのboxに共通部分でできるかどうかをチェックするために使用される。
:body [メソッド]
-
-
このbounding-boxによって内包される立方体を表現する
bodyを返す。
:init vlist &optional tolerance [メソッド]
-
-
minpointとmaxpointスロットをvlistから設定する。
もし、torelanceが指定されたなら、このbounding-boxは
その量で増大される。
make-bounding-box points [tolerance] [関数]
-
-
pointsのリストの中から最小と最大の座標値を見つけ、
bounding-boxのインスタンスを作る。
bounding-box-union boxes [tolerance *contact-threshold*] [関数]
-
-
boxesの結合で表現されるbounding-boxのインスタンスを作る。
その結果は、toleranceによって拡張される。
bounding-box-intersection boxes [tolerance *contact-threshold*] [関数]
-
-
boxesの共通領域を表現するbounding-boxのインスタンスを作る。
その結果は、toleranceによって拡張される。
2016-04-05
 (v1
(v1 v2)。
v1,v2とnormalは正規ベクトルでなければならない。
normalが与えられないとき、v1,v2の共通垂線の正規ベクトルが
使用される。この場合、結果は0から
v2)。
v1,v2とnormalは正規ベクトルでなければならない。
normalが与えられないとき、v1,v2の共通垂線の正規ベクトルが
使用される。この場合、結果は0から p1)
p1) p1))
p1)) num1 num2 [(tolerance *epsilon*)] [関数]
num1 num2 [(tolerance *epsilon*)] [関数]
 num2-toleranceである。
num2-toleranceである。
 num2+toleranceである。
num2+toleranceである。