逆運動学

ここで, エンドエフェクタの位置・姿勢は関節角度ベクトルを用いて

$\displaystyle \mbox{\boldmath {$r$}}$ $\displaystyle =$ $\displaystyle \mbox{\boldmath {$f$}}$ $\displaystyle ($ $\displaystyle \mbox{\boldmath {$\theta$}}$ $\displaystyle )$

(1)

$\displaystyle \mbox{\boldmath {$\theta$}}$ $\displaystyle =$ $\displaystyle \mbox{\boldmath {$f$}}$ $\displaystyle ^{-1}($ $\displaystyle \mbox{\boldmath {$r$}}$ $\displaystyle )$

(2)

における $f^{-1}$ は一般に非線形な関数となる. そこでを時刻tに関して微分することで, 線形な式

$\displaystyle \dot{\mbox{\boldmath {$r$}}}$	$\displaystyle =$	$\displaystyle \frac{\partial \mbox{\boldmath {$f$}}}{\partial \mbox{\boldmath {$\theta$}}} (\mbox{\boldmath {$\theta$}})\dot{\mbox{\boldmath {$\theta$}}}$	(3)
	$\displaystyle =$	$\displaystyle \mbox{\boldmath {$J$}}$ $\displaystyle ($ $\displaystyle \mbox{\boldmath {$\theta$}}$ $\displaystyle )\dot{\mbox{\boldmath {$\theta$}}}$	(4)

ヤコビ行列が正則であるとき逆行列 $\theta$ $)^{-1}$ を用いて以下のようにしてこの線型方程式の解を得ることができる.

$\displaystyle \dot{\mbox{\boldmath {$\theta$}}} = \mbox{\boldmath {$J$}}(\mbox{\boldmath {$\theta$}})^{-1}\dot{\mbox{\boldmath {$r$}}}$

(5)

しかし, 一般にヤコビ行列は正則でないので, ヤコビ行列の疑似逆行列 $^{\char93 }($ $\theta$ が用いられる(Equation

$\displaystyle \mbox{\boldmath {$A$}}$ $\begin{displaymath}^{\char93 } = \left\{ \begin{array}{l l} & \mbox{\boldmath {$... ...}^T \ ( m > n = rank \mbox{\boldmath {$A$}}) \end{array}\right.\end{displaymath}$

(6)

Equation

は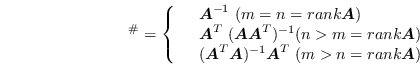，のときはEquation

を，のときはEquation

を，最小化する最小二乗解を求める問題と捉え,解を得る.

$\displaystyle \min_{\dot{\mbox{\boldmath {$\theta$}}}} \left(\dot{\mbox{\boldma... ...ath {$J$}}(\mbox{\boldmath {$\theta$}})\dot{\mbox{\boldmath {$\theta$}}}\right)$

(7)

$\displaystyle \min_{\dot{\mbox{\boldmath {$\theta$}}}}$		$\displaystyle \dot{\mbox{\boldmath {$\theta$}}}^{T}\dot{\mbox{\boldmath {$\theta$}}}$	(8)
$\displaystyle s.t.$		$\displaystyle \dot{\mbox{\boldmath {$r$}}} = \mbox{\boldmath {$J$}}(\mbox{\boldmath {$\theta$}})\dot{\mbox{\boldmath {$\theta$}}}$

$\displaystyle \dot{\mbox{\boldmath {$\theta$}}} = \mbox{\boldmath {$J$}}^{\char... ...mbox{\boldmath {$J$}}(\mbox{\boldmath {$\theta$}})\right)\mbox{\boldmath {$z$}}$

(9)

しかしながら, Equation

に従って解を求めると, ヤコビ行列 $\theta$ がフルランクでなくなる特異点に近づくと, $\left\vert\dot{\mbox{\boldmath {$\theta$}}}\right\vert$ が大きくなり不安定な振舞いが生じる. そこで, Nakamura et al.のSR-Inverse⁴を用いることで, この特異点を回避する.

本研究ではヤコビ行列の疑似逆行列 $^{\char93 }($ $\theta$ の代わりに, Equation

に示す $^{*}($ $\theta$ を用いる.

$\displaystyle \mbox{\boldmath {$J$}}$ $\displaystyle ^{*}($ $\displaystyle \mbox{\boldmath {$\theta$}}$ $\displaystyle ) =$ $\displaystyle \mbox{\boldmath {$J$}}$ $\displaystyle ^T\left(\mbox{\boldmath {$J$}}\mbox{\boldmath {$J$}}^T + \epsilon \mbox{\boldmath {$E$}}_m\right)^{-1}$

(10)

これは, Equation

の代わりに, Equation

を最小化する最適化問題を解くことにより得られたものである.

$\displaystyle \min_{\dot{\mbox{\boldmath {$\theta$}}}} \{ \dot{\mbox{\boldmath ... ... {$J$}}(\mbox{\boldmath {$\theta$}})\dot{\mbox{\boldmath {$\theta$}}}\right) \}$

(11)

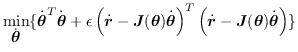
ヤコビ行列 $\theta$ が特異点に近づいているかの指標には可操作度 $\kappa($ $\theta$ ⁵が用いられる(Equation

$\displaystyle \kappa($ $\displaystyle \mbox{\boldmath {$\theta$}}$ $\displaystyle ) = \sqrt{\mbox{\boldmath {$J$}}(\mbox{\boldmath {$\theta$}}) \mbox{\boldmath {$J$}}^{T}(\mbox{\boldmath {$\theta$}})}$

(12)

微分運動学方程式におけるタスク空間次元の選択行列⁶は見通しの良い定式化のために省略するが, 以降で導出する全ての式において適用可能であることをあらかじめことわっておく.