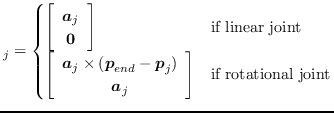一次元対偶を関節に持つマニピュレータのヤコビアンは
基礎ヤコビ行列7により
計算することが可能である.
基礎ヤコビ行列の第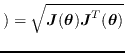 関節に対応するヤコビアンの列ベクトル
関節に対応するヤコビアンの列ベクトル
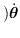
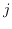 は
は
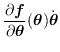 ![$\displaystyle _j= \begin{cases}\left[ \begin{array}{ccc} \mbox{\boldmath {$a$}}...
...\boldmath {$a$}}_j \end{array} \right] & \text{if rotational joint} \end{cases}$](jmanual-img159.png) |
(13) |
と表される.
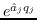
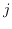 ・
・
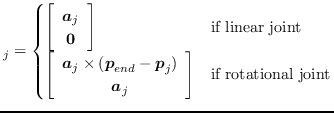
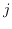 はそれぞれ第
はそれぞれ第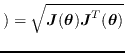 関節の関節軸単位ベクトル・位置ベクトルであり,
関節の関節軸単位ベクトル・位置ベクトルであり,
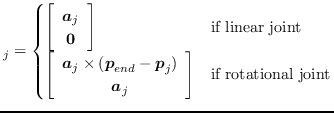
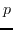 はヤコビアンで運動を制御するエンドエフェクタの位置ベクトルである.
上記では1自由度対偶の
回転関節・直動関節について導出したが,
その他の関節でもこれらの列ベクトルを
連結した行列としてヤコビアンを定義可能である.
非全方位台車の運動を表す2自由度関節は
前後退の直動関節と
旋回のための回転関節から構成できる.
全方位台車の運動を表す3自由度関節は
並進2自由度の直動関節と
旋回のための回転関節から構成できる.
球関節は姿勢を姿勢行列で,
姿勢変化を等価角軸変換によるものとすると,
3つの回転関節をつなぎ合わせたものとみなせる.
はヤコビアンで運動を制御するエンドエフェクタの位置ベクトルである.
上記では1自由度対偶の
回転関節・直動関節について導出したが,
その他の関節でもこれらの列ベクトルを
連結した行列としてヤコビアンを定義可能である.
非全方位台車の運動を表す2自由度関節は
前後退の直動関節と
旋回のための回転関節から構成できる.
全方位台車の運動を表す3自由度関節は
並進2自由度の直動関節と
旋回のための回転関節から構成できる.
球関節は姿勢を姿勢行列で,
姿勢変化を等価角軸変換によるものとすると,
3つの回転関節をつなぎ合わせたものとみなせる.
2016-04-05
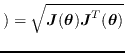 関節に対応するヤコビアンの列ベクトル
関節に対応するヤコビアンの列ベクトル
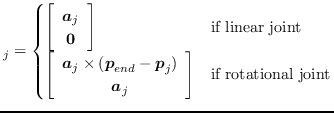
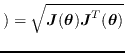 関節の関節軸単位ベクトル・位置ベクトルであり,
関節の関節軸単位ベクトル・位置ベクトルであり,