Next: 衝突回避計算例 Up: ロボットの動作生成 Previous: 衝突回避を含む逆運動学 Contents Index
![[*]](crossref.png) で得られる.
以下では
で得られる.
以下では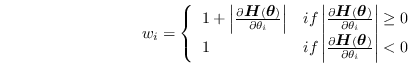 の添字は衝突回避計算のための成分を表し,
の添字は衝突回避計算のための成分を表し,
blending係数![]() は,
リンク間距離
は,
リンク間距離![]() と閾値
と閾値![]() ・
・![]() の関数として計算される
(Equation
の関数として計算される
(Equation ![[*]](crossref.png) ).
).
![]() は衝突回避計算を行い始める値
(yellow zone@xdefthefnmark
は衝突回避計算を行い始める値
(yellow zone@xdefthefnmark![[*]](crossref.png) footnotemark)であり,
footnotemark)であり,
![]() は目標タスクを阻害しても衝突回避を行う閾値
(orange zone@xdefthefnmark
は目標タスクを阻害しても衝突回避を行う閾値
(orange zone@xdefthefnmark![[*]](crossref.png) footnotemark)である.
footnotemark)である.
衝突計算をする2リンク間の最短距離・最近傍点が計算できた場合の 衝突を回避するための動作戦略は 2リンク間に作用する仮想的な反力ポテンシャルから導出される.
2リンク間の最近傍点同士をつなぐベクトル
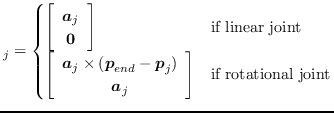 を用いた
2リンク間反力から導出される速度計算を
Equation
を用いた
2リンク間反力から導出される速度計算を
Equation ![[*]](crossref.png) に記す.
に記す.