Next: 重心ヤコビアン Up: ロボットの動作生成 Previous: マスプロパティ計算 Contents Index
第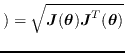 関節の運動変数を
関節の運動変数を![]() とする.
まず,回転・並進の1自由度関節を考える.
とする.
まず,回転・並進の1自由度関節を考える.
![]()
![]()
ここで,
![]() は
AddMassProperty関数に第
は
AddMassProperty関数に第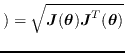 関節の子リンクより
末端側のリンクのマスプロパティを与えたものであり,
実際には再帰計算により計算する17.
これらを
関節の子リンクより
末端側のリンクのマスプロパティを与えたものであり,
実際には再帰計算により計算する17.
これらを
![]() で割ることにより
ヤコビアンの各列ベクトルを得る.
で割ることにより
ヤコビアンの各列ベクトルを得る.
![]()
![]()
これより慣性行列は次のように計算できる.
| (34) |
| (35) |
 軸,
回転関節
軸,
回転関節 軸を
もつと考え整理し,次のようになる.
軸を
もつと考え整理し,次のようになる.
| (36) |
![\begin{displaymath}\left[
\begin{array}{c}
\mbox{\boldmath {$P$}}\\
\mbox{\bold...
...$}}_{B}\\
\dot{\mbox{\boldmath {$\theta$}}}
\end{array}\right]\end{displaymath}](jmanual-img264.png) |
(37) |
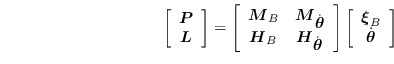 ,
重心位置
,
重心位置
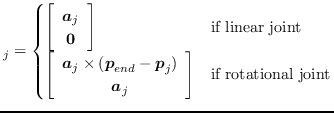
| (38) |