基本bodyの作成関数

make-plane &key :normal :point :distance [関数]

pointを通り，normalの方向を向いたplaneオブジェクトを作る。 pointを与える代わりdistanceを指定することもできる。

*xy-plane* [変数]

*yz-plane* [変数]

*zx-plane* [変数]

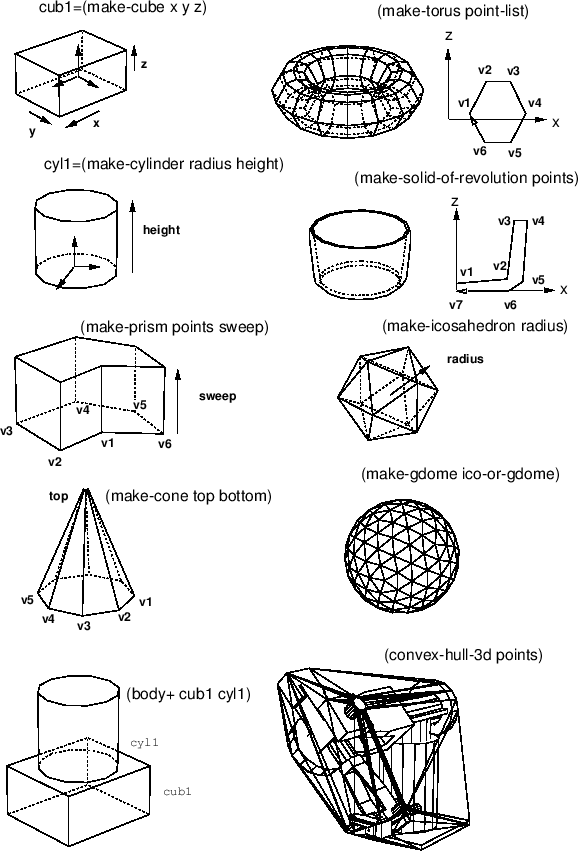
Figure: 基本body

make-cube xsize ysize zsize &key :name :color [関数]

x,y,z軸の方向に大きさがxsize,ysize,zsizeである，直方体を作る。 この直方体の原点はbodyの中心に置かれる。

make-prism bottom-points sweep-vector &key :name :color [関数]

sweep-vectorに沿ったbottom-pointsにより定義される 形状を積み上げることにより角柱を作る。 もし、sweep-vectorが実数ベクトルでなく数字であれば、$z$方向の 角柱の高さとして扱われる。 bottom-pointsは，このbodyの底面を定義する順番になっていなければならない。 例えば， (make-prism '(#f(1 1 0) #f(1 -1 0) #f(-1 -1 0) #f(-1 1 0)) 2.0) は，高さ2.0の直方体を作る。

make-cylinder radius height &key (:segments 12) :name :color [関数]

半径radiusと高さheightで指定される円柱を作る。 底面は，xy-平面に定義され，座標系の原点は底面の中心に置かれる。

make-cone top bottom &key (:segments 16) :color :name [関数]

頂点がtopで底面がbottomである角錐を作る。 topは，3次元ベクトルである。 bottomは，底面の頂点のリストあるいは半径である。 もし，頂点のリストなら，順番を慎重にしなさい。   (make-cone #f(0 0 10) (list #f(10 0 0) #f(0 10 0) #f(-10 0 0) #f(0 -10 0)))  は，正方形の底面を持つ四角錐を作る。

make-solid-of-revolution points &key (:segments 16) :name :color [関数]

pointsは，z軸まわりの時計方向に回転される。 もし、pointsのリストの2つの端点がz軸上に置かれてないならば， 曲面を作る。したがって， (make-solid-of-revolution '(#f(0 0 1) #f(1 0 0))) は、円錐を作り、 (make-solid-of-revolution '(#f(1 0 1) #f(1 0 0))) は、円柱を作る。 pointsは、順番が重要であり、$z$軸の高い方から低い方へ 整列しておくことが望まれる。

make-torus points &key (:segments 16) :name :color [関数]

ドーナッツのようなtorus形状を作る。 pointsは，断面上の頂点のリストである。

make-icosahedron &optional (radius 1.0) [関数]

正20面体を作る。それぞれの面は正三角形である。

make-dodecahedron &optional (radius 1.0) [関数]

正12面体を作る。それぞれの面は，正五角形である。

make-gdome abody [関数]

abodyの三角面を4つの面に小分けすることにより 測地ドームを新しく作る。 abodyは，最初正20面体とすべきである。 それから，make-gdomeの結果を再帰的にmake-gdomeに与えることができる。 それぞれの呼び出しで，測地ドームの面の数は，4倍に増加する。すなわち， 20, 80, 320, 1280, 5120などになる。

(setq g0 (make-icosahedron 1.0))        ; 20 facets
(setq g1 (make-gdome g0))               ; 80 facets
(setq g2 (make-gdome g1))               ; 320 facets
...

grahamhull vertices &optional (normal #f(0 0 1)) [関数]

Grahamのアルゴリズムを用いて，2次元上で凸状の覆いを計算する。 quickhullよりも遅い。

quickhull vertices &optional (normal #f(0 0 1)) [関数]

2分探索法を用いて2次元上で凸状の覆いを計算する。

convex-hull-3d vertices [関数]

gift-wrapping法を用いて3次元上で凸面の覆いを計算する。

make-body-from-vertices vertices-list [関数]

矛盾しない順番になっている面のループを定義する頂点のリストからbodyを返す。